Некоторые модели параллельных программ
Развитие точных методов в программировании привело к возникновению различных формальных моделей программ, в том числе и моделей параллельных программ.
Рассмотрим модели параллельных программ, прототипом которых явились операторные схемы программ, в частности схемы Янова.
В.Е.Котовым и А.С.Нариньяни была предложена формальная модель параллельных вычислений, названная асинхронной моделью.
Асинхронная программа над памятью M (A-программа) представляет собой множество X блоков и массивов блоков. Блок x образован парой (y, 0), где y – предикат над MCÌM, MC – управляющая память, O – оператор над памятью M. С O-оператором связаны входные и выходные наборы переменных из М. По входному набору О-оператор вычисляет значение переменных выходного набора. Предикат y – спусковая функция блока x.
Кроме асинхронной программы, в понятие асинхронной модели входит и асинхронная система. Асинхронная система представляет собой совокупность правил, позволяющих для заданной асинхронной программы X и заданного начального значения памяти M осуществить некоторый процесс вычислений.
Чтобы получить более формальное определение пары "программа–система", вводится конструкция метасистемы, которая сопоставляет каждому начальному состоянию памяти некоторое множество вычислительных процессов. Приведем некоторые понятия и обозначения.
Пусть A – множество операторов над памятью M.
Для каждого момента t множество операторов вычислительного процесса можно разбить на 4 непересекающихся множества:
+At – включающиеся в t;
-At – выключающиеся в t;
pAt – находящиеся во включенном состоянии;
0At – находящиеся в выключенном состоянии.
Q = {q} – множество состояний метасистемы, q0 – начальное состояние.
F – функция, однозначно сопоставляющая каждому множеству

y – функция, ставящая в соответствие каждому набору


включительно).
Каждому оператору aiÎA сопоставляется счетчик ci с начальным значением Æ.
Текущее значение счетчика ci фиксирует разность между числом имевших место включений и числом имевших место выключений
оператора ai.
Тогда модель Котова–Нариньяни можно записать в виде рекурсивных соотношений:
qt = Y(M0, P||t-1); |
At=At-1\+At-1È-At-1; |
*At=F1(0At, qt); |
+At Í *At; |
рAt=рAt-1\-At-1È +At; |
-At Í рAt. |
1. М – множество ячеек памяти.
2. A={a,b,...} – конечное множество операторов; для каждого оператора из А заданы:
K(a) – количество символов выключения оператора a (целое положительное число);
Д (а) £ М – множество входных ячеек оператора а;
Т (а) £ М – множество выходных ячеек оператора а.
3.Четверка Г = (а, q0,S,t) – управление схемы,
где q0 – выделенное начальное состояние.
При этом каждому оператору а сопоставлены один символ включения


где


t – функция переходов – частичная функция из QxS в Q, всюду определенная на QxSt.
Управление Г формирует последовательность выполнения операторов. Элементы из Si обозначают акты включения операторов, элементы из St – акты выключения. Включение оператора а допустимо лишь в таком состоянии q, что значение t
(q, a) определено. После включения оператора завершение его работы допустимо в произвольном состоянии, поскольку функция t всюду определена на QxSt. При включении оператор а использует значения ячеек из Д (а), при выключении он засылает свои результаты в ячейки из Т(а) и формирует символ выключения, который соответствует одному из K(а) направлений условной передачи.
Полезным для эффективного распознавания свойств параллельных схем программ является класс счетчиковых схем.
Счетчиковой схемой называется схема R=(M, A, Г ), для которой управление Г задается следующим образом.
Пусть k – целое неотрицательное число;
S – конечное множество;
S – множество с выделенным элементом S0;
pÎNk, где Nk – множество неотрицательных целых чисел;
v – функция из S в Nk, такая, что если sÎSt, то v(s)³0;
q: SxS®S – частичная функция, всюду определенная на SxSt.
Полагая, что значение t((S,x),s) определено, если определено q(S,s) и выполнено x+v(s)³0. Если значение определено, то полагается
t((S,x),s)=(q(S,s), x+v(s)).
Более простыми и наглядными являются параллельные операторные схемы – частный случай счетчиковых схем.
Параллельной операторной схемой называется произвольная счетчиковая схема, обладающая следующими свойствами:
1) S = {S0};
2) для каждого sÎS значение q(S0,s) определено;
3) если s – символ выключения, то каждая компонента вектора v(s) равна 0 или 1;
4) если s – символ включения, то каждая компонента вектора v(s) равна 0 или -1;
5) для любых двух неравных символов включения s, s¢ из
v(s)i= -1 следует v(s¢)i=0.
Параллельную операторную схему можно представить в виде ориентированного графа с операторными вершинами Оа, Оb, Оc,... и вершинами-счетчиками d1, d2, ..., dk. Каждый счетчик di помечается числом pi, которое является начальным значением этого счетчика. Дуги графа направлены либо от операторных вершин к счетчикам, либо от счетчиков к операторным вершинам. Дуги сопоставлены ненулевым компонентам векторов v(s).
Если (v(aj))i=1, то выключение оператора а с символом выключения aj увеличивает значение счетчика i на 1. Если (v(

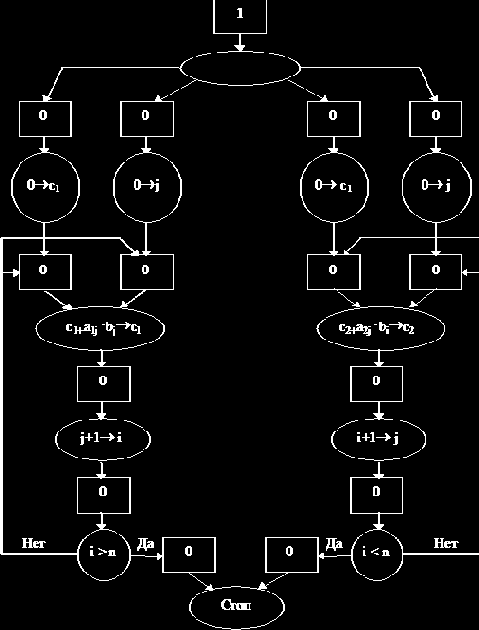
Пример. Пусть необходимо перемножить матрицу


а результат поместить в (с1, с2).
Графовое представление некоторой интерпретированной операторной схемы, задающей алгоритм умножения, будет иметь следующий вид
(рис. 8.5).
Рассмотрим теперь другие модели программ, которые в меньшей мере опираются на понятие операторных схем программ.
В качестве модели программы иногда предлагается пара R=(M,C), где M определяет ее информационную, а С – управляющую структуру. Для представления информационной структуры М используются простые вычислительные модели, а для представления управляющей структуры – сети Петри. Сеть Петри – двудольный граф, множество вершин которого состоит из переходов tjÎT и позиций piÎP. Кроме того, заданы две функции инцидентности:
|
F : PxT®{0,1}; |
|
B : TxP®{0,1}. |
"p(N¢(p)=N(p)–F(p,t)+B(p,t)).
Переходы срабатывают последовательно, но недетерминированно. Сеть останавливается, если при некоторой разметке ни один из переходов не может срабатывать.
Сети Петри используются также для описания различных типов управления. Здесь тип управления задает семейство регулярных абстрактных структур управления. По уровням рассматриваются базовые средства управления следующих классов:
 |
· безусловные, которые не зависят от текущих значений переменных в исполняемой программе;
· условные, которые принимают во внимание текущие значения
данных.
Для исследования операционных проблем параллельного программирования удобной явилась модель UCLA-граф. UCLA-граф представляет собой ориентированный граф, вершины которого соответствуют операторам параллельной программы, дуги – управляющим или информационным связям между операторами.С каждой вершиной связаны входное управление и выходное управление, каждое из которых может быть двух типов – конъюнктивное и дизъюнктивное. При дизъюнктивном входном управлении выполнение оператора может начаться в том случае, если "активизируется" одна и только одна из дуг, входящих в эту вершину – оператор. В случае конъюнктивного входного управления выполнение оператора может начаться в том случае, если активизированы все дуги, заходящие в вершину. После завершения исполнения вершины с дизъюнктивным входным управлением активизируется одна и только одна из дуг, исходящая из вершины. В случае конъюнктивного выходного управления активизируются все дуги, исходящие из вершины. Существенным недостатком UCLA-графов является требование развертки циклов.
