Отношение предшествования процессов
В научной литературе исследуются различные подходы к выделению и описанию параллельных процессов. В связи с этим рассмотрим различные типы параллелизма.
Впервые, по-видимому, мы услышали о параллельном программировании в 1958 г. после выхода статьи Гилла (S. Gill) "Параллельные программы". Если система имеет только одну начальную (В) и только одну конечную (F) вершину (арех), то отношения предшествования, которые возможны между процессами p1, p2, ... , pn, показаны на рис. 8.1.
Каждый граф на рис. 8.1 описывает трассу развития процесса во времени и указывает на отношение предшествования. Такие графы называют графами развития процесса.
Пример 1. Вычислить значение выражения
| (a+ b) • (c + d) – (e/f) | (1) |
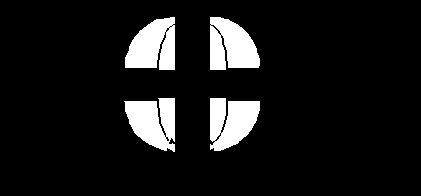 |
Если точность вычисления значения выражения или другие побочные эффекты не предполагают иного порядка выполнения операций, то вычисления могут производиться параллельно.
Рис. 8.1. Граф развития процесса:
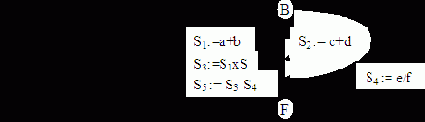 |
а – последовательные процессы;б – параллельные процессы;
в – последовательно-параллельные процессы
| Рис. 8.2. Дерево для выражения (1) | Рис. 8.3. Граф развития процесса для вычисления выражения (1) |
Н. Вирт (1966) предложил для описания параллелизма использовать простую конструкцию and. Тогда предложения программы для вычисления выражения (1) (рис. 8.3) могут быть следующими:
begin
S1: = a + b and S2: = c + d and S4: = e/f;
S3: = S1 • S2;
S5: = S3 – S4
end.
С логической точки зрения каждый процесс имеет собственный процессор и программу. Реально два различных процесса могут разделять одну и ту же программу или один и тот же процессор. Например, для вышеприведенной задачи два разных процесса используют одну и ту же программу "сложить (+)". Таким образом, процесс не эквивалентен программе.
В качестве упражнения полезно построить граф развития процесса для примеров 2 и 3 и решить пример 4.
Пример 2. Сортировка слиянием. Во время i-го прохода в стандартной сортировке слиянием второго порядка пары сортируемых списков длины 2i–1 сливаются в списке длины 2i. Все слияния в пределах одного прохода могут быть выполнены параллельно.
Пример 3. Умножение матриц. При выполнении умножения матриц A = B • C, все элементы матрицы A могут быть вычислены одновременно.
Пример 4. Оценить требуемое минимальное время как функцию n для вычисления выражения a1 + a2 + ... + an , n ³ 1, в предположении, что:
* параллельно может быть выполнено любое число операций
сложения;
* каждая операция (включая выборку операндов и запись результата) занимает одну единицу времени.
